因果推断导论笔记-Lecture5-Model-Based Inference for Completely Randomized Experiments

基于模型的推断（参数模型）。

课前两道题

也就是说，上节课的回归模型也是非参的。

如果样本量小，正态性其实不满足了，会出现问题。

以前三种方法的弊端

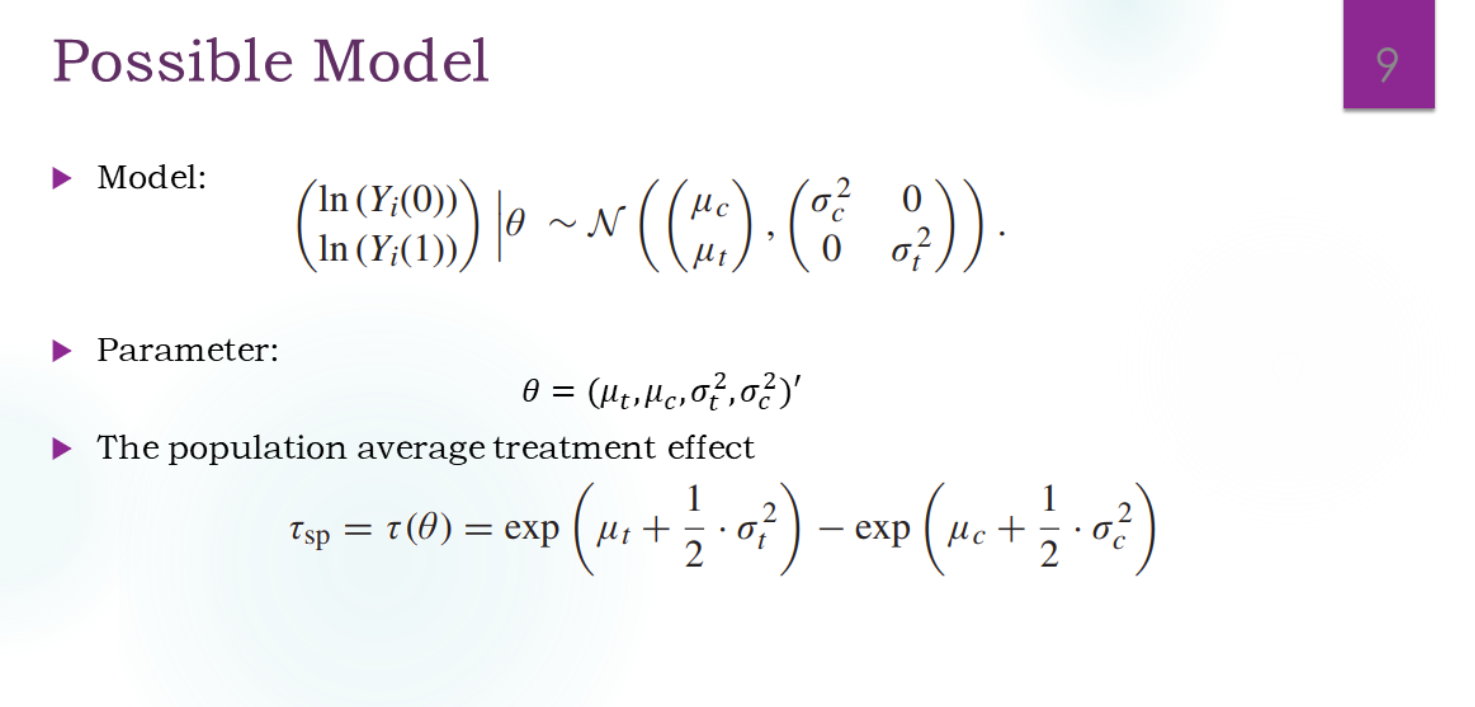
小样本下，为了正态可能需要进行转换。如上图的ln。

但是这样的话$τ_{sp}$可能不是无偏了，因为期望和对数指数不能随意互换。

因此引入了参数模型。本质上是一种贝叶斯的方法。

考试最多要求binomial和normal模型

动机

背景：无限总体的完全随机试验。

目标：有限总体ACE：$τ_{fs}=τ(Y(0),Y(1))$

​ 无限总体ACE：$τ_{sp}=τ(θ)$

对于有限总体：

$$Y_i(0)=W_iY_i^{mis}+(1-W_i)Y_i^{obs}\\ Y_i(1)=(1-W_i)Y_i^{mis}+W_iY_i^{obs}$$

所以$τ_{fs}=\hatτ(Y^{obs},\hat Y^{mis}, W)$

如何填补$Y^{mis}$？

1.用均值填补，没有随机性，方差是0。

2.随机抽样来填补。也有方差了。

贝叶斯学派把原来看作是标量的$τ_{fs}$看成是变量了。

贝叶斯框架简介

和频率学派最大的区别是：把未知的参数看作随机变量。

P(θ)是对参数的先验认知。这是一个假设。

用p(data | θ)来推p(θ|data)，这时就可以用这个式子算看到的θ的概率了。

$$P(θ|Y)=\frac{P(Y|θ)P(θ)}{P(Y)}\\$$

而传统频率学派得到的都是参数的点估计，对应的是贝叶斯得到的概率分布的峰值。

总结就是：

Bayesian Model-based Imputation-Theory

三种情形。

No Correlation, No Covariates（需要重点掌握）

这种方法是：填补的数据用模型来生成。

最终的目标是：$f(τ|Y^{obs},W)$

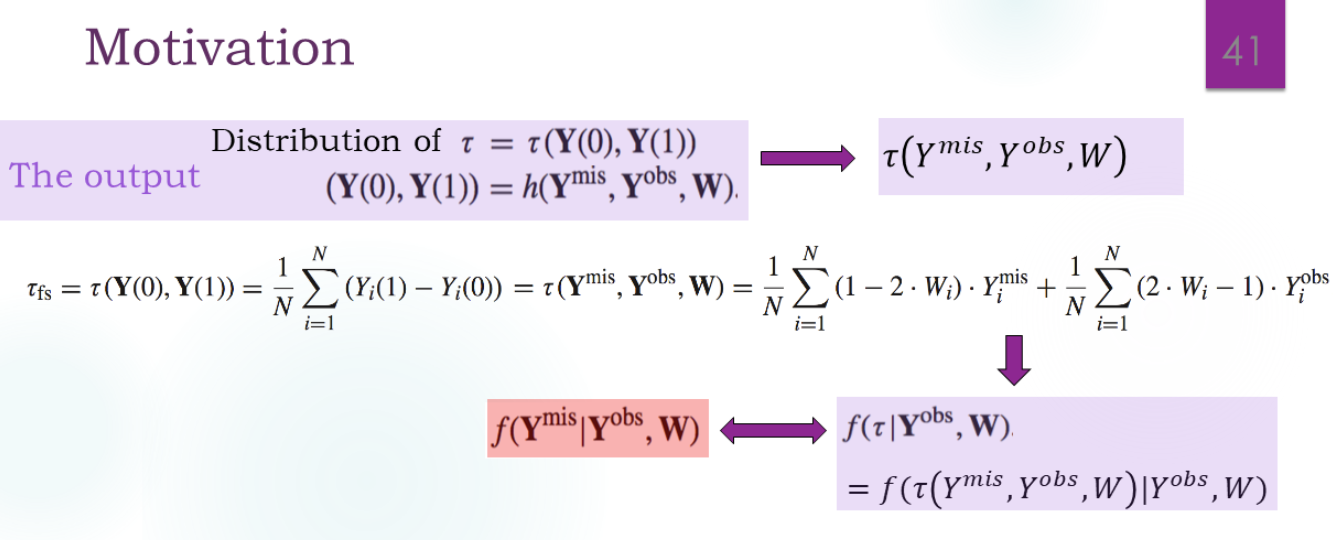
已知$f(Y|θ)，P(θ)，P(W|Y)$，这里Y是向量。

由于W和Y，θ独立，所以$f(Y|θ)=f(Y|W, θ)$

$(Y^{mis}_i, Y^{obs}_i)$和$(Y_i(0),Y_i(1))$差一个线性变换。

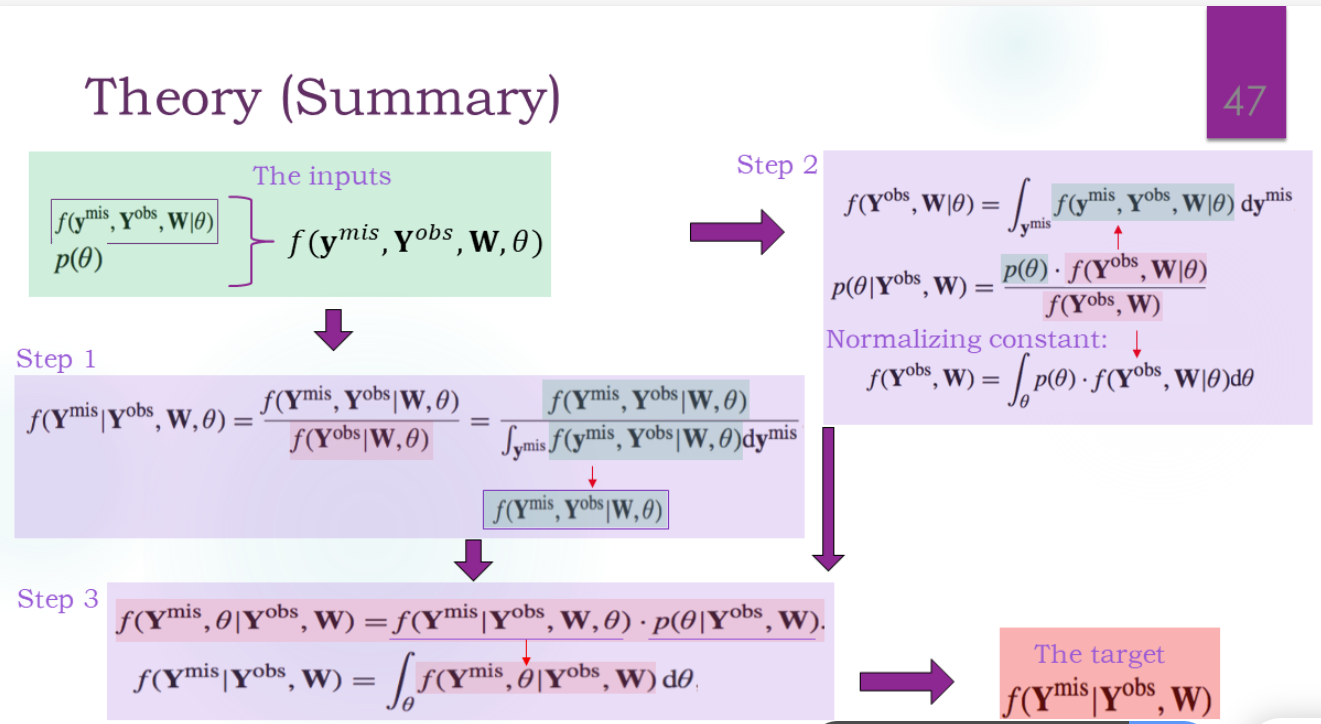
实例

有空看看，主要是识别核心项，用到了多元正态的知识（死去的记忆x）：

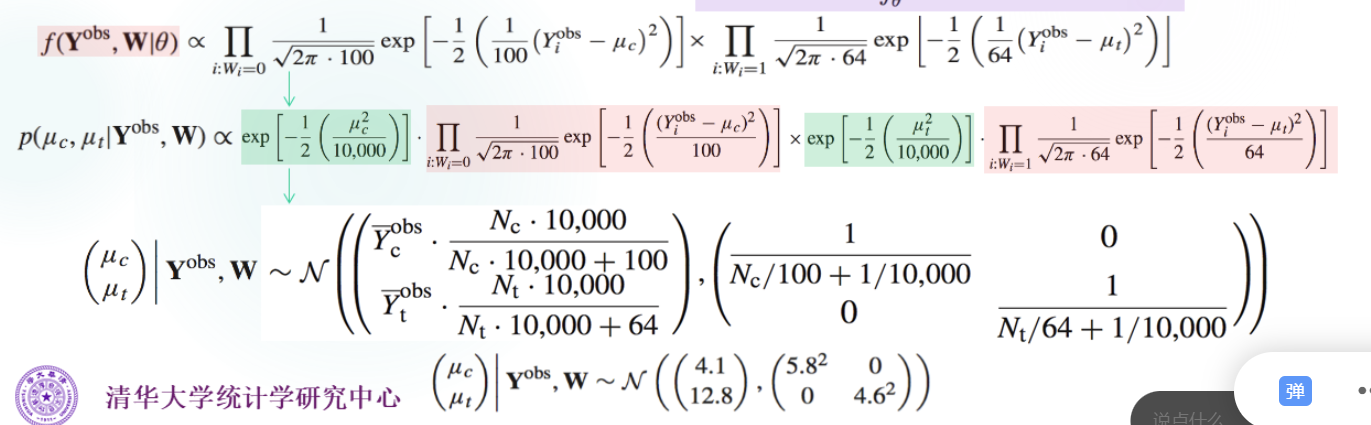
上面得到了$Y^{mis}=Bθ$

$E_A(Y^{mis})=E_A(E(Y^{mis}|θ))=E_A(Bθ)$

Correlation, No Covariates

相关系数ρ同样是一个参数。

数据无法帮助我们更新ρ的后验分布。

Correlation, Covariates

略

Simulation

推断后验需要识别核心项。

通过样本能得到经验分布函数，大数定理趋近于CDF。

通过θ的后验step1取一个θ值，然后计算θ条件下$Y^{mis}$的分布step2。抽一个$Y^{mis}$，就得到了一个样本。样本可以计算τ，然后就得到了τ的分布。

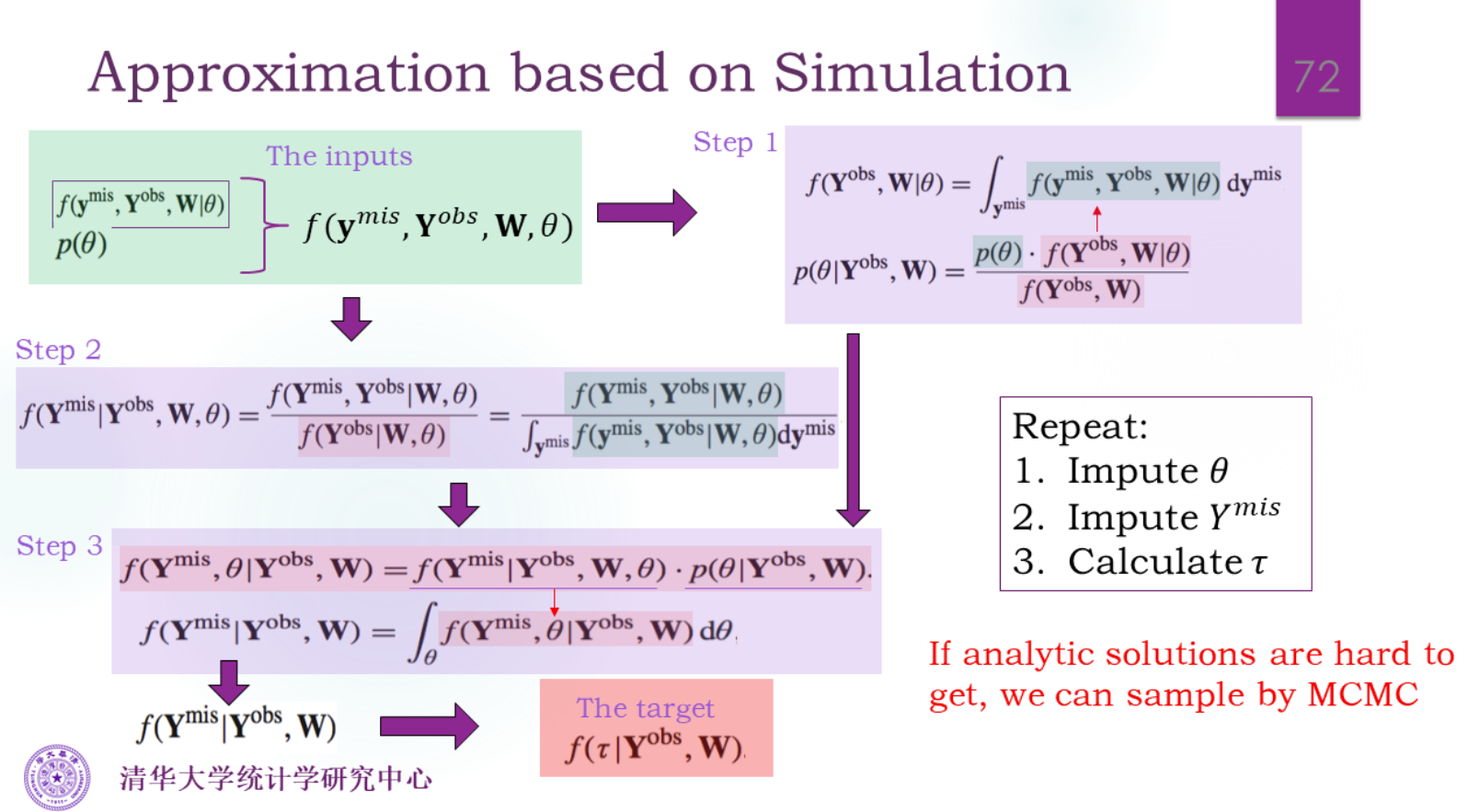
Super Population下

就比较简单了，不需要填补$Y^{mis}$：

各种模型：